嵌入模型

先决条件

文档

注意

This conceptual overview focuses on text-based embedding models.

Embedding models can also bemultimodal though such models are not currently supported by LangChain.

想象一下能够将任何文本——一条推文、一份文档或一本书——捕捉成一种单一、紧凑的表示形式。这就是嵌入模型的强大之处，它们是许多检索系统的核心。嵌入模型将人类语言转化为机器能够理解并快速准确地进行比较的一种格式。这些模型接收文本作为输入，并输出一个固定长度的数字数组，这是文本语义意义的数字指纹。嵌入使得搜索系统不仅可以基于关键词匹配，还可以基于语义理解来查找相关文档。

关键概念

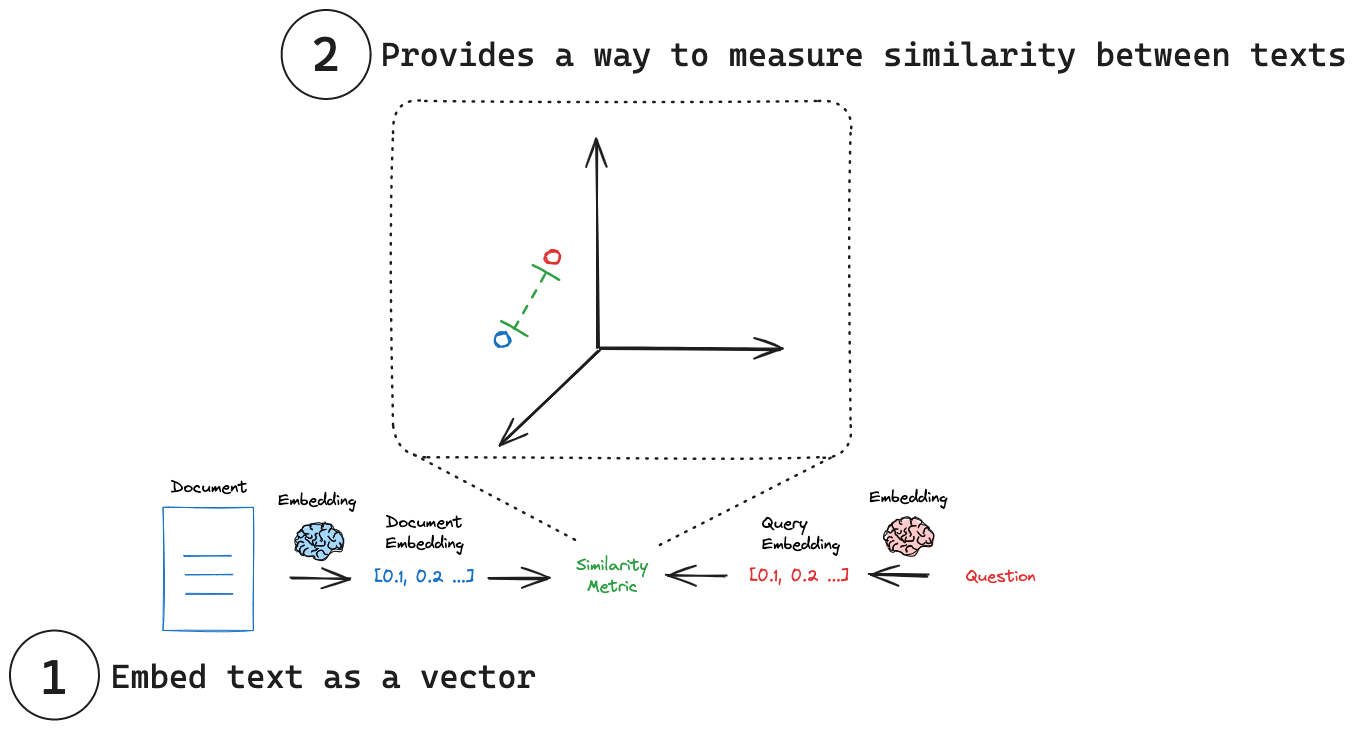
Conceptual Overview

(1) 将文本嵌入为向量: 嵌入将文本转换为数值向量表示。

(2) 衡量相似度: 可以使用简单的数学运算来比较嵌入向量。

嵌入

历史背景

多年来，嵌入模型领域取得了显著的进步。 2018年，Google推出了BERT（Bidirectional Encoder Representations from Transformers），这是一个重要的里程碑。 BERT将Transformer模型应用于文本嵌入，生成简单的向量表示，在各种自然语言处理任务中取得了前所未有的性能。然而，BERT在高效生成句子嵌入方面并非最优。这一限制促生了SBERT（Sentence-BERT）的诞生，它对BERT架构进行了调整，以生成语义丰富的句子嵌入，这些嵌入可以通过余弦相似度等相似性指标轻松进行比较，极大地降低了查找相似句子等任务的计算开销。如今，嵌入模型生态系统非常多样化，众多提供商都推出了自己的实现。为了在这些模型中进行导航，研究人员和实践者经常转向诸如Massive Text Embedding Benchmark（MTEB）此处这样的基准测试来进行客观比较。

接口

LangChain提供了一个通用的接口来处理它们，为常用操作提供了标准方法。这个通用接口通过两个核心方法简化了与各种嵌入提供商的交互：

embed_documents: 用于嵌入多个文本（文档）
embed_query: 用于嵌入单个文本（查询）

这种区分很重要，因为一些提供商对要搜索的文档和搜索输入本身（查询）采用了不同的嵌入策略。为了说明这一点，这里有一个使用LangChain的.embed_documents方法嵌入字符串列表的实际示例：

from langchain_openai import OpenAIEmbeddings
embeddings_model = OpenAIEmbeddings()
embeddings = embeddings_model.embed_documents(
    [
        "Hi there!",
        "Oh, hello!",
        "What's your name?",
        "My friends call me World",
        "Hello World!"
    ]
)
len(embeddings), len(embeddings[0])
(5, 1536)

API Reference:OpenAIEmbeddings

为了方便起见，您还可以使用embed_query方法来嵌入单个文本：

query_embedding = embeddings_model.embed_query("What is the meaning of life?")

集成

LangChain提供了许多嵌入模型的集成，您可以在嵌入模型集成页面上找到它们。

衡量相似度

每个嵌入本质上是一组坐标，通常位于高维空间中。在这个空间中，每个点（嵌入）的位置反映了其对应文本的含义。就像相似的词在词汇表中彼此靠近一样，相似的概念在这个嵌入空间中也彼此靠近。这使得对不同文本片段进行直观的比较成为可能。通过将文本简化为这些数值表示，我们可以使用简单的数学运算来快速衡量两段文本的相似程度，而无论它们原始的长度或结构如何。一些常见的相似性度量包括：

余弦相似度 (Cosine Similarity)：测量两个向量之间夹角的余弦值。
欧几里得距离 (Euclidean Distance)：测量两点之间的直线距离。
点积 (Dot Product)：测量一个向量在另一个向量上的投影。

相似性度量的选择应基于所使用的模型。例如，OpenAI在其嵌入中建议使用余弦相似度，这可以轻松实现：

import numpy as np

def cosine_similarity(vec1, vec2):
    dot_product = np.dot(vec1, vec2)
    norm_vec1 = np.linalg.norm(vec1)
    norm_vec2 = np.linalg.norm(vec2)
    return dot_product / (norm_vec1 * norm_vec2)

similarity = cosine_similarity(query_result, document_result)
print("Cosine Similarity:", similarity)

关键概念​

嵌入​

历史背景​

接口​

集成​

衡量相似度​

关键概念

嵌入

历史背景

接口

集成

衡量相似度